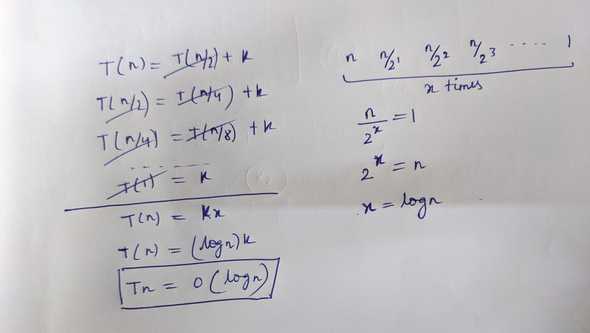« Theoretical analysis for time taken by recursion algorithm

Time complexity analysis for Factorial using recursion

T(n) = k1 + k2 + T(n-1)

=> T(n) = k + T(n-1)

=> T(n) = T(n-1) + k

T(n) = T(n-1) + k

T(n-1) = T(n-2) + k

T(n-2) = T(n-3) + k

...

T(1) = T(0) + k;

T(0) = k;

Add all the above mentioned

T(n) = k(n+1)

T(n) = kn + k

T(n) = kn

T(n) = O(n)

So, for factorial time complexity will be O(n)

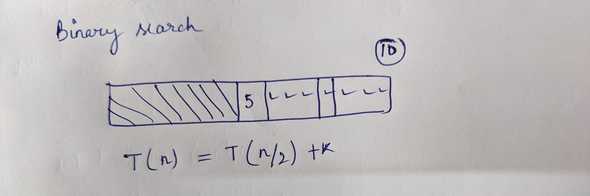
Time complexity analysis for Binary search using recursion

T(n) = k + T(n/2)

T(n/2) = k + T(n/4)

T(n/4) = k + T(n/8)

...

T(1) = k

Adding all above gives

T(n) = kx

x = log(n)

T(n) => O(log(n))

log(n) is a very fast algorithm

for 10⁶ elements we only need to perform 20 searches.