« Theoretical analysis for time taken by algorithm

Theoretical analysis.

BIG O notation

Lets suppose

Algorithm 1: 10n² +5n + 8

Algorithm 2: 5n² + 2n + 1000

for n -> 10n² and 5(n²) will dominate

We can't actually say Algorithm 2 will take 5(n²) time complexity. Ss this is going to change based on system. We can never actually say time. We can just convey how many instructions(addition and subtraction and if blocks and comparisons) it will take.

10⁵ operations will remain same for all the systems, only thing will change is how much time its going to take on different systems.

5(n²) here n² will change, 5 is just a constant so we will ignore 5 also.

Note:

1. We will talk only about number of operations and not time.
2. We will focus on highest power term.
3. We won't care about the coefficient much.

algorithm A -> O(f(n))

Algorithm A is called Big O of f(n) if time taken by algorithm A for input n <= k * f(n)

For example :

Algorithm 2 takes f(n) = 5n² + 10n + 1000 <= 6n²

so Algorithm 2 is O(n²)

Time complexity for finding largest element in array

max=a[0]

if(max<a[i]){

Copy
1max = a[i]

}

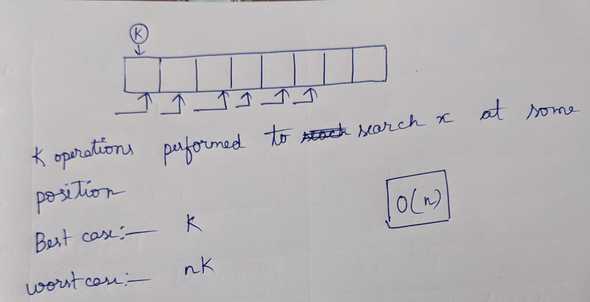
Time taken = (k operations) n times

Time taken <= (k+1)*n

Time complexity = O(n)

Time complexity for Bubble sort an array

Each time we perform k steps for n-1 comparisons

then k steps for n-2 comparisons

then k steps for n-3 comparisons

bubble sort => (n-1)k + (n-2)k + (n-3)k + (n-4)k + (n-5)k + ...... + k

bubble sort => (k)(n-1)(n)/2 => k(n²/2) - k(n/2) => (k/2)(n²) => c(n²)

time taken bubble sort => c(n²)

so bubble sort is O(n²)

All these are called theoretical analysis.

Linear search Time complexity

Insertion sort time complexity

Best case: O(n)

Worst case: O(n²)

Selection sort time complexity

Best case: O(n²)

Worst case: O(n²)