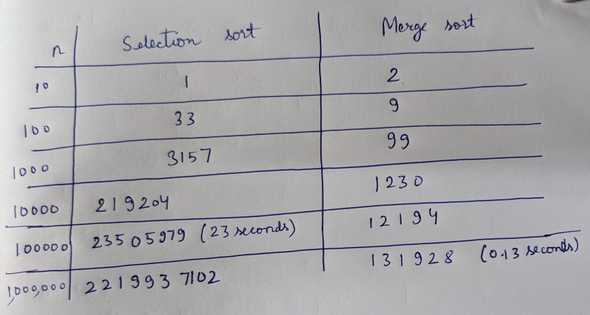
« Experimental analysis for time taken by algorithm

What is time complexity analysis

Idea is to figure out how good or bad the solution is in terms of time & space required. In general we try to find worst cases as we want to be sure our algorithm performs well in worst cases also.

Cons of experiment analysis:

1. If we run our program again it will give different result

   Reason: when we run our program it is not the only program that runs. How much time processor will give to my program and other similar reasons will tell us how much time our program will take on the exact same input.

2. Test case generation. Reason:

   Copy
   11 2 3 4 5
   2
   3Insertion sort: very fast
   4
   5Selection sort: slow
   6
   7Insertion sort and selection sort are almost same time complexity algorithm but some test cases favour particular algorithms.

3. If a problem comes and I figured out 10 solutions. How will I figure out which is better. I have to write code for each of them.

4. Time consuming. Selection sort might take minutes and hours to sort 10 million integers.

Time taken by Merge sort for sorting certain size array

Copy
1#include <iostream>
2#include <iomanip>
3#include <algorithm>
4#include <string>
5#include <cstring>
6#include <vector>
7#include <cmath>
8#include <map>
9#include <climits>
10#include <sys/time.h>
11// climits for INT_MIN
12#include <unordered_map>
13using namespace std;
14
15long timeInMicroseconds()
16{
17    struct timeval start;
18    gettimeofday(&start, NULL);
19    return (start.tv_sec * 1000000 + start.tv_usec);
20}
21
22void merge(int arr[], int start, int mid, int end)
23{
24    int n1 = mid - start + 1;
25    int n2 = end - mid;
26
27    int L[n1], R[n2];
28
29    for (int i = 0; i < n1; i++)
30    {
31        L[i] = arr[start + i];
32    }
33    for (int j = 0; j < n2; j++)
34    {
35        R[j] = arr[mid + 1 + j];
36    }
37
38    int i = 0;
39    int j = 0;
40    int k = start;
41
42    while (i < n1 && j < n2)
43    {
44        if (L[i] <= R[j])
45        {
46            arr[k] = L[i];
47            i++;
48        }
49        else
50        {
51            arr[k] = R[j];
52            j++;
53        }
54        k++;
55    }
56
57    while (i < n1)
58    {
59        arr[k] = L[i];
60        i++;
61        k++;
62    }
63
64    while (j < n2)
65    {
66        arr[k] = R[j];
67        j++;
68        k++;
69    }
70}
71
72void mergeSort(int *arr, int start, int end)
73{
74    if (start >= end)
75    {
76        return;
77    }
78    int mid = (start + end) / 2;
79    mergeSort(arr, start, mid);
80    mergeSort(arr, mid + 1, end);
81    merge(arr, start, mid, end);
82}
83
84int main()
85{
86    for (int n = 10; n <= 1000000; n *= 10)
87    {
88        int *arr = new int[n];
89        long startTime, endTime;
90        for (int i = 0; i < n; i++)
91        {
92            arr[i] = n - i;
93        }
94        startTime = timeInMicroseconds();
95        mergeSort(arr, 0, n - 1);
96        endTime = timeInMicroseconds();
97        cout << "Merge sort for n = " << n << " size time= " << (endTime - startTime) << endl;
98    }
99    return 0;
100}

Time taken by Selection sort for sorting certain size array

Copy
1#include <iostream>
2#include <iomanip>
3#include <algorithm>
4#include <string>
5#include <cstring>
6#include <vector>
7#include <cmath>
8#include <map>
9#include <climits>
10#include <sys/time.h>
11// climits for INT_MIN
12#include <unordered_map>
13using namespace std;
14
15long timeInMicroseconds()
16{
17    struct timeval start;
18    gettimeofday(&start, NULL);
19    return (start.tv_sec * 1000000 + start.tv_usec);
20}
21
22void selectionSort(int arr[], int n)
23{
24    for (int j = 0; j < n - 1; j++)
25    {
26        int min = arr[j];
27        int pos = j;
28        for (int i = j + 1; i < n; i++)
29        {
30            if (arr[i] < min)
31            {
32                min = arr[i];
33                pos = i;
34            }
35            int temp = arr[j];
36            arr[j] = min;
37            arr[pos] = temp;
38        }
39    }
40}
41
42int main()
43{
44    for (int n = 10; n <= 1000000; n *= 10)
45    {
46        int *arr = new int[n];
47        long startTime, endTime;
48        for (int i = 0; i < n; i++)
49        {
50            arr[i] = n - i;
51        }
52        startTime = timeInMicroseconds();
53        selectionSort(arr, n);
54        endTime = timeInMicroseconds();
55        cout << "Merge sort for n = " << n << " size time= " << (endTime - startTime) << endl;
56    }
57    return 0;
58}